Solving Logistic Regression with Coordinate Descent in Three ways
Introduction
In this article, we consider a standard unconstrained optimization problem on solving logistic regression with heart disease data set:
\[min L(w)\]where \(L(·)\) is some cost function and \(w \in \mathbb{R}^d\). In class, we looked at several approaches to solving such problems—such as gradient descent and stochastic gradient descent—under differentiability conditions on \(L(w)\). We will now look at a different, and in many ways simpler, approach:
- Initialize \(w\) somehow.
- Repeat: pick a coordinate \(i \in \{1, 2, ... , d\}\), and update the value of \(w_i\) so as to reduce the loss.
Two questions need to be answered in order to fully specify the updates:
- Which coordinate to choose?
- How to set the new value of \(w_i\)?
Description of coordinate descent method
Key Strategies:
- Objective function(Loss function) and gradients:
The Maximum likelihood estimation of logistic regression is in a form of:
\[L(w) = -1/n\displaystyle\sum_{i=1}^{n} y_{i} \log \hat{y}_{i} + (1 - y_{i}) \log(1 - \hat{y}_{i})\]We transform \(\hat y = w^T x_i +b\) by a Sigmoid function \(\sigma(x)=\frac{1}{1+e^{-x}}\), hence, the loss function can be writen as:
\[L(w) = -1/n\displaystyle\sum_{i=1}^{n} y_{i} \log \sigma(\hat{y}_{i}) + (1 - y_{i}) \log(1 - \sigma(\hat{y}_{i}))\]Thus, the coordinate gradient with respect with each weight \(w_{j}\) is given by
\[\frac{\partial L(w)}{\partial w_{j}} = \displaystyle \sum_{i=1}^{n}(\sigma(\hat{y}_{i}) - y_{i})x_{j}\]- Rules for selecting coordinates:
- randomly pick a coordinate \(i\) at a time
- Cyclic coordinate descent: go through all the features cyclically. (1,2,..13,1,2,…13,1,2…until converge.)
- Gauss-Southwell Method: at each iteration, pick coordinate \(i\) that has greatest gradient in absolute value for which:
- Rules for updating \(\omega_i\):
Here, \(\eta\) denotes step size.
- Constraint on loss function: L(·) should be convex and differentiable.
Convergence
Under what conditions do you think our method converges to the optimal loss?
The objective function(Loss function) values are non-decreasing: \(f(x(0)) \geq f(x(1)) \geq f(x(2)) ...\), if \(f\) is strictly convex and differentiable, the algorithm converges to a global minimum. Hence, we we let iterations keep going until the loss gets as close to as \(L^*\), which is the fitting Loss of our baseline logistic regrssion model.
We will take the difference between fitting loss and \(L^*\), if the difference is less than \(0.001\), we will consider the fitting process converged to a gloabal minimum, then the iterations will terminate.
Experiment Results
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import log_loss
from sklearn.metrics import accuracy_score
- Prepare data
data = np.loadtxt('heart.csv', delimiter=',', skiprows=1)
X, y = data[:, :-1], data[:,-1]
# normalize features
X = (X - X.mean(axis=0))/(X.max(axis=0) - X.min(axis=0))
# add intercept-1 vector to feature matrix
X = np.hstack((X, np.ones((X.shape[0], 1))))
# examine data
print(X.shape)
print(np.ones((X.shape[0], 1)).shape)
Output:
(303, 14)
(303, 1)
- Baseline Loss on Logistic Regression
Begin by running a standard logistic regression solver(not regularized) on the training set. Make note of the final loss \(L^*\).
# baseline logistic regression model without regularization
reg = LogisticRegression(solver='sag', C=100000, max_iter = 10000).fit(X, y)
L_base = log_loss(y, reg.predict_proba(X))
print(f"Baseline(Logistic Regression) Training Loss L* = {L_base}")
Output:
Baseline(Logistic Regression) Training Loss L* = 0.3489042453037286
Then, implement your coordinate descent method and run it on this data.
- Implementing CoordinateDescent Classifier.
class CoordinateDescent():
def __init__(self, target, select, step=0.01):
"""Create a Coordinate Descent Classifier.
"""
self.target = target
self.step = step
self.select = select
def __sigmoid(self, x):
"""Squashing function.
"""
return 1 / (1 + np.exp(-x))
def fit(self, X, y):
"""Update coefficient based on different strategy of selecting one coordinate each time.
Fitting process will be ended while converging criteria met.
"""
self.n_features = X.shape[1]
w = np.zeros(self.n_features).reshape(self.n_features, 1)
self.L = []
diff = 1
cycle_digit = 0
self.num_iter = 0
while diff >= 0.001:
y_hat = self.__sigmoid(np.dot(w.T, X.T))
loss = -(1 / X.shape[0]) * np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat))
self.L.append(loss)
delta = list(np.dot((y_hat - y), X)[0]) # gradients
cycle_index = cycle_digit % X.shape[1]
if self.select == 'cgd': # select with largest gradient in absolute value
to_update = np.argmax(np.abs(delta))
w[to_update] = w[to_update] - self.step * delta[to_update]
elif self.select == 'rand': # randomly select coordinate
random = np.random.randint(0,13)
w[random] = w[random] - self.step * delta[random]
elif self.select == 'cycle': # cyclic go through all coordinate
w[cycle_index] = w[cycle_index] - self.step * delta[cycle_index]
cycle_digit += 1
self.num_iter += 1
diff = loss - self.target
self.w = w
return self
def predict(self, X):
"""Calculate OLS result with coefficients trained by fittting.
"""
y_pred = self.__sigmoid(np.dot(self.w.T, X.T))
y_pred = np.array(list(map(lambda x: 1 if x >= 0.5 else 0, y_pred.flatten())))
return y_pred
def get_loss(self):
return self.L
def get_coef(self):
return self.w
def get_num_iter(self):
return self.num_iter
- Method 1: Cyclic go through each coordinate \(i\)
# fit training data with coordinate descent model(default 1050 iterations)
m1 = CoordinateDescent(target=L_base, select='cycle').fit(X, y)
m1_pred = m1.predict(X)
# Accuracy
m1_acc = accuracy_score(y, m1_pred)
# Training Loss
L1 = m1.get_loss()
num_iter1 = m1.get_num_iter()
print(f"Go through each coordinate cyclically: \n\
-------------------------------------- \
\nAccuracy: -> {m1_acc} \
\nFitting Loss: -> {L1[-1]} \
\n#Iterations: -> {num_iter1}")
Output:
Go through each coordinate cyclically:
--------------------------------------
Accuracy: -> 0.8514851485148515
Fitting Loss: -> 0.349902342590921
#Iterations: -> 3576
- Method 2: Pick coordinate \(i\) that has greatest gradient in absolute value at each iteration
# fit training data with coordinate descent model
m2 = CoordinateDescent(target=L_base, select='cgd').fit(X, y)
m2_pred = m2.predict(X)
# Accuracy
m2_acc = accuracy_score(y, m2_pred)
# Training Loss
L2 = m2.get_loss()
num_iter2 = m2.get_num_iter()
print(f"Select feature based on largest gradient: \n\
----------------------------------------- \
\nAccuracy: -> {m2_acc} \
\nFitting Loss: -> {L2[-1]} \
\n#Iterations: -> {num_iter2}")
Output:
Select feature based on largest gradient:
-----------------------------------------
Accuracy: -> 0.8382838283828383
Fitting Loss: -> 0.3499040333347324
#Iterations: -> 1622
- Finally, compare to a method that chooses coordinates \(i\) uniformly at random, we’ll call this “random-feature coordinate descent”.
m3 = CoordinateDescent(target=L_base, select='rand').fit(X, y)
m3_pred = m3.predict(X)
# Accuracy
m3_acc = accuracy_score(y, m3_pred)
# Training Loss
L3 = m3.get_loss()
num_iter3 = m3.get_num_iter()
print(f"Randomly select coordinate: \n\
---------------------------------- \
\nAccuracy: -> {m3_acc} \
\nFitting Loss: -> {L3[-1]} \
\n#Iterations: -> {num_iter3}")
Output:
Randomly select coordinate:
----------------------------------
Accuracy: -> 0.8514851485148515
Fitting Loss: -> 0.3499041459249309
#Iterations: -> 4893
Conclusion
Three different methods all converged to \(L^*\) within a sufficiently small range, however, they do take different number of iterations to achieve their results, apparently selecting coordinate based on the largest coordinate gradient requires the smallest number of iterations(\(1622\)), which indicating this method converging faster than the others, respectively, cyclic coordinate gradient takes \(3576\) iterations, random selecting takes \(4800-5500\) times, for random selecting, even though the number of iterations may differ each time, the difference is trivial.
We visualize this result by plotting the fitting curves below.
def plot_loss():
plt.figure(figsize=(10,6))
plt.plot(L1, 'green', label='"Cyclic Coordinate Descent"')
plt.plot(L2, 'red', label='"Coordinate Gradient Descent"')
plt.plot(L3, 'orange', label='"Random Coordinate Descent"')
plt.axhline(y=L_base, color='lightblue', label='Baseline L*')
plt.title('Coordinate Descent Fitting Loss', fontsize=16)
plt.xlabel('Iterations', fontsize=16)
plt.ylabel('Fitting Loss', fontsize=16)
plt.xticks(fontsize=12)
plt.yticks(fontsize=12)
plt.legend(prop={'size': 16})
plot_loss()
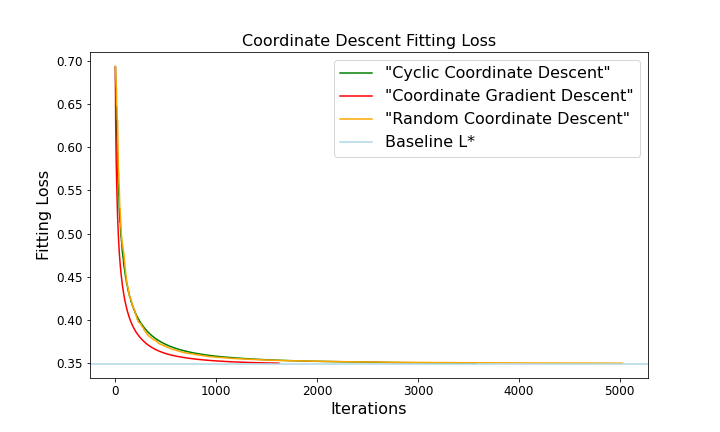
The graph above shows how the loss of our “adaptive” coordinate descent algorithm’s current iterate—that is, \(L(w_t)\)—decreases with \(t\); it should asymptote to \(L^*\). Also, it shows the corresponding curve for random-feature coordinate descent.